Neste guia completo, vamos explorar passo a passo como construir o gráfico de uma função matemática. Vamos abordar desde a definição da função até a representação visual da mesma no plano cartesiano.
Definição da Função Matemática
Uma função matemática é uma relação entre um conjunto de entradas, chamado domínio, e um conjunto de saídas, chamado contradomínio. Matematicamente, uma função \( f \) é representada pela notação \( f(x) \), onde \( x \) é a variável independente.
Passos para Construir o Gráfico da Função
1. Identificar o Domínio e Contradomínio
Antes de construir o gráfico, é fundamental identificar o domínio e o contradomínio da função. O domínio é o conjunto de todas as possíveis entradas da função, enquanto o contradomínio é o conjunto de todas as possíveis saídas.
2. Escolher Pontos de Referência
Selecionar alguns valores para a variável independente \( x \) e calcular os correspondentes valores da função \( f(x) \). Estes pares ordenados \( (x, f(x)) \) serão os pontos que iremos plotar no gráfico.
3. Plotar os Pontos no Plano Cartesiano
Utilizando um sistema de coordenadas cartesianas, onde o eixo horizontal representa o domínio da função e o eixo vertical representa o contradomínio, plotamos os pontos selecionados.
4. Traçar a Curva da Função
Conectar os pontos plotados com uma linha suave, formando assim o gráfico da função. É importante lembrar que em alguns casos, como funções não lineares, pode ser necessário plotar mais pontos para obter uma representação precisa da curva.
Exemplo de Gráfico de uma Função Quadrática
Vamos considerar a função quadrática \( f(x) = x^2 \) como exemplo. Seguindo os passos acima, podemos construir seu gráfico da seguinte maneira:
Claro! Aqui está a transformação do diagrama em uma tabela:
| ( x ) | ( f(x) ) |
|---|---|
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
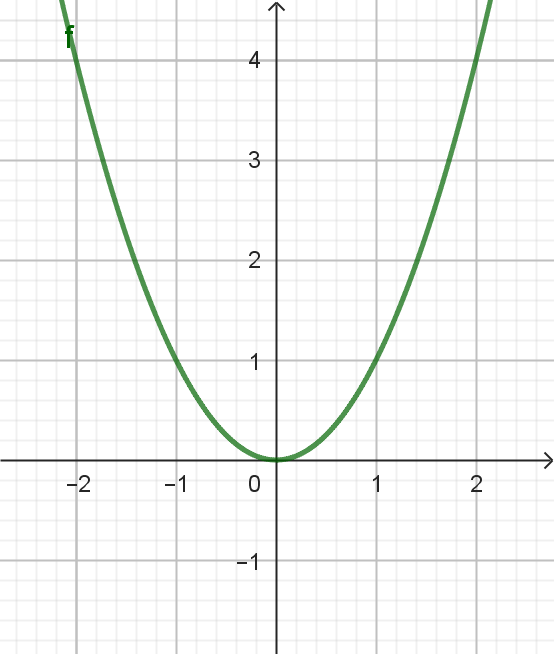
No gráfico acima, os pontos foram plotados e conectados para formar a curva da função quadrática \( f(x) = x^2 \).
Conclusão
Construir o gráfico de uma função matemática pode ser uma tarefa desafiadora, mas seguindo os passos corretos, é possível representar visualmente o comportamento da função de forma clara e precisa.
Lembrando sempre de identificar o domínio e o contradomínio, escolher pontos de referência, plotar os pontos no plano cartesiano e traçar a curva da função. Com este guia completo, esperamos que você possa construir gráficos de funções com confiança e precisão.
