Conceito de conjunto
Conjuntos são uma parte fundamental da Matemática. Muitos aspetos que se estudam em Matemática e em outras disciplinas têm as suas bases no conceito de conjunto.
No dia-a-dia deparamo-nos com vários objectos e animais que apresentam propriedades comuns. No estudo dos conjuntos, esses objectos e animais podem ser agrupados tendo em conta estas características que lhes são comuns.
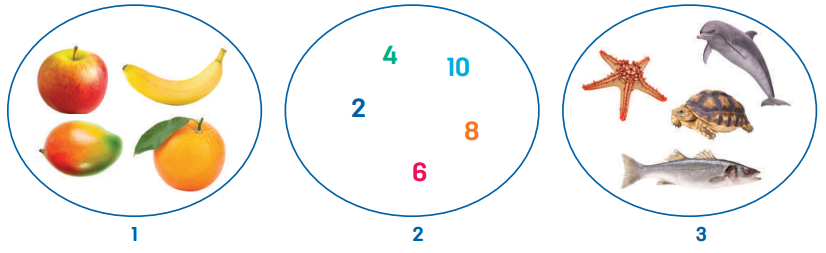
Um conjunto é uma coleção de objetos com determinada característica comum. A cada objeto de um conjunto chama-se elemento do conjunto.
Conjunto 1 – representa frutas: banana, maçã, manga, laranja.
Conjunto 2 – representa números pares até 10.
Conjunto 3 – representa animais marinhos: peixe, estrela-do-mar, tartaruga, golfinho.
Como podes observar no exemplo acima, os objectos foram agrupados segundo uma característica comum. Podemos definir um conjunto, como sendo qualquer colecção de objectos com uma propriedade comum. Cada um desses objectos é chamado elemento do conjunto.
Exemplos de conjuntos:
a) O conjunto formado pelas vogais do nosso alfabeto.
b) O conjunto dos números naturais.
c) O conjunto de colegas da tua turma.
d) O conjunto de membros da tua família de casa.
e) O conjunto formado pelas cores da Bandeira Nacional.
Nota: Os elementos de um conjunto podem ser números, letras, pessoas, animais, plantas, objectos, entre outros
Exemplos de Elementos de um Conjunto
Conjunto das cores da bandeira de Moçambique é constituído pelas cores: verde, branca, preta, amarela e vermelha.
Então, a cor vermelha é elemento do conjunto das cores da bandeira..
Conjunto de números pares menores que 10 é composto pelos números: 0, 2, 4, 6 e 8. Então, 2 é um elemento do conjunto dos números pares menores que 10.
No conjunto de vogais do alfabeto temos a, e, i, o, u. Assim, a é um elemento deste con- junto.
Relação de pertença: Relação entre conjuntos e elementos
Quando um objecto é um dos elementos de um conjunto, dizemos que este objecto pertence ao conjunto. Caso contrário, dizemos que não pertence ao conjunto. Para representarmos esta relação,usamos os símbolos ∈ e ∉.
O símbolo ∈ lê-se pertence e o símbolo ∉ lê-se não pertence.
Para indicar que um elemento x pertence ao conjunto A, escrevemos:
x ∈ A: lê-se x pertence ao conjunto A.
Para indicar que um elemento y não pertence ao conjunto A, escrevemos:
y ∉ A: lê-se y não pertence ao conjunto A.
Exemplo: Considera o conjunto B = {a, e, i, o, u}. Então:
$a ∈ B; \ i ∈ B, \ b ∉ B; \ d ∉ B$ ou $ a, i ∈ B; \ b, d ∉B $
Designação/ Notação dos conjuntos e seus elementos
Geralmente, usam-se letras maiúsculas do nosso alfabeto, A, B, C, D e outras, para denotar os conjuntos. Os elementos de um conjunto são denotados por letras minúsculas.
Representação dos conjuntos
Os conjuntos podem ser representados de duas formas: Em chavetas ou em diagrama de Venn.
O número de elementos de um conjunto chama-se cardinal do conjunto e representa-se por # ou n.
Chavetas { }
Exemplo 1: O conjunto A formado pelas vogais do nosso alfabeto. A sua representação por chavetas pode ser: A = {a, e, i ,o, u}
Exemplo 2: o conjunto E formado pelas cores da bandeira de Angola. A sua representação por chavetas pode ser: E = {amarela, vermelha, preta}.
Exemplo 3: O conjunto B formado pelos números naturais até 10. A sua representação por chavetas pode ser: B= {1, 2, 3, 4, 5, 6, 7,8, 9, 10}
Diagrama de Venn
Para além das chavetas, os conjuntos também podem ser representados por diagramas, conhecidos como diagramas de Venn. Esta forma de representar os conjuntos deve-se ao filósofo inglês John Venn (1834-1883).
Os diagramas de Venn podem ser representados por círculos, rectângulos, triângulos ou qualquer curva fechada, como podemos observar a seguir:

Definição de um conjunto: por extensão e por compreensão
Existem duas formas de definir um conjunto: Definição por extensão e definição por compreensão.
a) Na definição por extensão, os elementos do conjunto são apresentados de maneira explícita dentro de chavetas e separados por vírgula. No diagrama de Venn, cada ele- mento é associado a um ponto.
Exemplos:
I ={1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
V = {a, e, i, o , u}
b) Na definição por compreensão, refere-se a propriedade comum dos seus elementos.
Exemplos:
I ={números ímpares menores que 20}
V = {vogais do alfabeto}
Exemplo 1: O conjunto C formado pelos números pares maiores que 10. A definição por compreensão pode ser: C = {n: n é um número par maior que 10}
Exemplo 2: O conjunto D formado por todas as consoantes do alfabeto. A sua definição por compreensão pode ser: D = {n: n é uma consoante}
Exemplo 3: O conjunto F formado pelas cores neutras. A sua definição por compreensão pode ser: E = {n: n é uma cor neutra}
Exercícios
- Representa em extensão ou em compreensão os seguintes conjuntos:
a) O conjunto A dos números ímpares entre 1 e 15.
b) B = {2, 4, 6, 8, 10} c) O conjunto C dos municípios da tua província.
d) D = {4, 8, 12} e) F = {1, 3, 5, 7, 9}
f) O conjunto H de todas as províncias do teu país.
g) O conjunto I das letras da palavra Matemática. - Representa por extensão os seguintes conjuntos:
a) O conjunto A formado pelas consoantes do nosso alfabeto.
b) O conjunto B dos números primos entre 1 e 10.
c) O conjunto C dos meses do ano com 31 dias.
d) O conjunto D dos meses do ano com 28 ou 29 dias.
e) O conjunto dos países pertencentes aos PALOP. - Representa por compreensão os seguintes conjuntos:
a) A = {1, 3, 6, 9, 12} d) D = {Abril, Junho, Setembro, Novembro}
b) B = {catana, roda dentada, estrela} e) E = {1, 2, 3, 6}
c) C = {10, 20, 30, 40, 50, 60, 70}
